안녕하세요. 백준 chogahui05입니다. RSA 알고리즘을 알기 위해서, 알아야 하는 것이 몇 가지 있는데요. 그 중 하나인 확장 유클리드 알고리즘을 알아보겠습니다. 사실 CRT라던지, 페르마의 소정리도 알아두면 좋기는 합니다. 이게 무엇을 구하는 것인지 알아보겠습니다.

a와 b가 매우 큰 수일 때, 이 값은 어떻게 구하는 것이 좋을까요? 일단, gcd(a,b)의 값이 k이고, k값이 1이 아니라고 해 봅시다. 그러면, a = ka', b = kb'으로 다시 쓸 수 있습니다.

gcd(a,b)값이 k이므로, a'과 b'도 정수입니다. x와 y가 정수라면 a'x + b'y도 정수입니다. 그러면, 1은 k의 배수여야 합니다. 그렇지 않습니다. 따라서, a와 b의 최대 공약수가 1이 아니라면, ax + by = 1을 만족하는 정수 (x,y)쌍은 존재하지 않습니다.
gcd(a,b)의 값이 1일 때, ax + by = 1을 만족하는 정수 (x,y)의 쌍 중 하나를 어떻게 구할까요?

a가 b보다 크거나 같은 정수라고 하겠습니다. 여기서 우리는 x'과 y'을 알 때, x와 y를 구하면 됩니다. 여기서, ax + by = 1은 정수해가 무수히 많이 나올 수도 있다는 점을 주의하세요. 즉, (x,y)쌍이 하나만 나올 수 있지 않고, 여러 개가 나올 수 있습니다. a = bQ + r 꼴로 나타낼 수 있다고 해 봅시다.

초록색 부분을 주의깊게 보면, bQx + by의 값은 b(Qx + y)로 나타낼 수 있습니다. 따라서, x' = Qx + y이고 , y' = x라면, bx' + ry'의 값은 1입니다. 우리는 x'과 y'을 알았을 때, x와 y값을 구하면서 올라와야 합니다. 따라서, x = y'이고, y = x' - Qx라고 할 수 있습니다. 여기서 Q의 값은 a를 b로 나누었을 때 몫입니다.
이것을 따져가면서 위로 올라가 보겠습니다. 먼저, gcd(a,b)값을 계속 호출해서, gcd(a',b')이 호출되었다고 해 봅시다. 이 때, b'은 0이고, a'은 0보다 큰 정수라고 해 보겠습니다. 예를 들어 a의 값이 7이고, b의 값이 5라고 해 보겠습니다.

그러면 계속 올라간다면, gcd(1,0)까지 도달하게 될 겁니다.

1x = 1에서, x의 값은 1입니다. 따라서, gcd(1,0)을 호출했을 때 x값은 1, y값은 0이 됩니다. 여기서, 출발해 보겠습니다.
먼저 a = 2, b = 1이라고 해 봅시다. 그러면 b = 1, r = 0이므로, 2x + y = 1, 1x' + 0y' = 1을 만족할 겁니다. 여기서, x'과 y'은 우리가 이미 알고 있는 값입니다. 이 값을 통해서, x와 y값을 구해야 합니다. x = y'이므로, x값은 다음과 같이 구할 수 있습니다.

다음에 y값은 x' - Qx입니다. x'의 값은 1이고, Q값은 2를 1로 나눈 몫인 2입니다. 그리고 x값은 0입니다.

즉, y값은 노란색으로 칠한 것에다가 보라색으로 칠한 a에다가, 보라색으로 칠한 b를 나눈 몫에다가 x를 곱한 값을 빼면 됩니다. 즉, 1에다가 2를 1로 나눈 몫에 0을 곱한 값을 빼면 되므로, 1이 됩니다. 검증해 보면, 2(0) + 1(1) = 1이니까 맞아요.

이제, 2x' + y' = 1의 해를 알 때, 5x + 2y = 1이 되는 (x,y)를 구해봅시다. 먼저, x값은 y'의 값을 그대로 가지고 오면 되므로, 1입니다.

y값이 문제인데요. x'값을 가져오면 0입니다. 그리고, 왼쪽 보라색 값인 5를 오른쪽 보라색 값인 2로 나누었을 때 몫인 2에다가, x값을 곱한 값은 2인데요. 0에서 이 값을 뺍니다. 그러면 -2가 나옵니다. 따라서, 5x + 2y = 1의 해 중 하나는 (1, -2)입니다. 이제, 5x + 2y = 1의 해를 알고 있습니다. 7x + 5y = 1의 해를 구해보겠습니다.

x' = 1, y' = -2입니다. 즉, 5x' + 2y' = 1을 만족시키는 해 중 하나가 (1,-2)라는 것을 알고 있을 때, 7x + 5y = 1을 만족시키는 해 (x,y)를 찾는 게 목표입니다. 먼저 x값은 y'의 값을 그대로 취하면 됩니다. 따라서, -2가 됩니다.
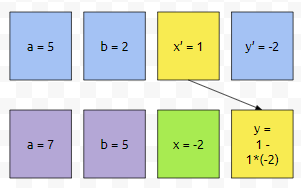
다음에 y값은, x'값인 1에서, 7을 5로 나눈 몫에 -2를 곱한 -2를 뺍니다. y값은 3이 됩니다. 7에 -2를 곱하면 -14입니다. 5에 3을 곱하면 15입니다. -14에 15를 더하면 1입니다. 그러면, 이 경우 시간 복잡도는 어떻게 될까요? 들어가는 수의 스케일이 작은 경우에는 많아봤자 재귀적으로 함수를 O(log(min(a,b)))만큼 부르게 되어 있습니다. 여기에, 더하고, 빼고, 곱하고, 나누는 연산의 복잡도를 곱하면 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| event driven : ps 문제에서 간단하게 활용해 봅시다. (0) | 2020.05.01 |
|---|---|
| 귀류법 : 명제가 거짓임을 가정한다. (6) | 2020.04.27 |
| 백준 공유기 설치 : 왜 이분탐색이 가능한가? (0) | 2020.03.27 |
| 플로이드 알고리즘 : 어떻게 최단거리가 갱신되는가? (9) | 2020.03.03 |
| 백준 화성지도 : 구간에 장벽을 세운다. (5) | 2020.02.24 |


최근댓글