예전에 vector가 인자로 들어왔을 때, 어떻게 해야 되는지를 올렸습니다. 어느 분이 댓글로 피드백을 주셨습니다. 그 내용에 관해서 보강 설명을 하도록 하겠습니다. 사실 동적 배열에서 중요한 것은 딱 3개입니다. capacity, size. 그리고 grow rate. ps를 하시다 보면, vector의 reserve와 resize 함수를 써야 하는 경우가 있습니다. 어떤 경우인지는 밑에서 설명해 드리도록 하겠습니다.
동적 배열의 기본 동작 먼저 설명해 드리겠습니다. 먼저, 4개의 원소를 저장할 수 있는 공간에 3개의 원소가 있다고 해 봅시다. 이 경우에, capacity는 4이고, size는 3입니다. 이걸 그림으로 나타내면 아래와 같습니다.

여기서, push_back(3)이 호출되면 어떤가요? 이 때에는 들어갈 자리가 있습니다. 그러니, [3]번째에 3을 넣습니다.

다음에 5를 넣을 겁니다. 그런데 들어갈 자리가 없어요. 이 때, expand 연산이 일어나는데요. 새로운 배열은 기존 배열의 몇 배의 크기를 잡을까요? 1.5배? 아니면 2배? 2배로 잡아 봅시다.

노란색 부분은 복사됩니다. 다음에, 5가 새로 생성된 배열의 [4]번째에 들어가면 좋겠군요.
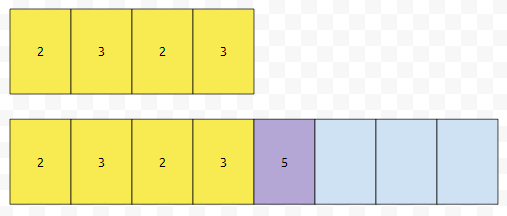
그 다음에, 기존에 있었던 4개 짜리는 이제 필요한가요? 그렇지 않습니다. 따라서, 제거합니다.
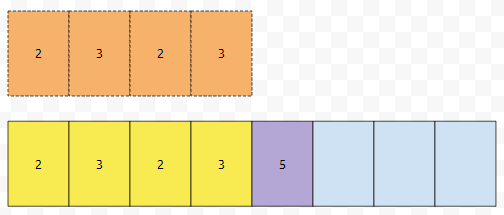
push_back(5)를 했을 때 일어난 상황입니다. 공간이 없으니까, 새롭게 공간을 할당해서 복사한 다음에, 기존에 있었던 공간은 제거한다. 이 expand 연산은 생각보다 비용이 많이 듭니다. grow rate는 제가 많이 언급을 했으니, 초기 size가 1인 dynamic array가 있다고 해 봅시다. 그리고 2^19+1번 push_back을 해 보도록 하겠습니다. 그러면 어떻게 될까요?

이 프로그램을 수행시켜 봅시다. 벡터의 초기 capacity는 구현체에 따라 다를 수도 있어요. 그런데, 제 환경에서는 초기 size는 0이였고, capacity는 1이였습니다. 그러면, 1, 2, 4, 8, 16, ... 이런 식으로 계속 커질 겁니다.
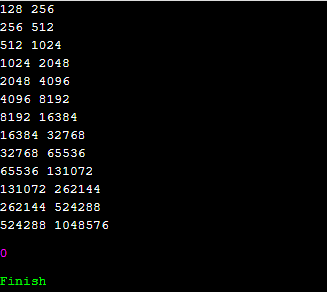
여기서, 맨 마지막 줄에 있는 524288과 1048576을 봅시다. 이 중 중요한 수는 뒤의 1048576입니다. 저는 분명 2^19 + 1개의 원소를 v에 넣었는데, v의 용량은 1048576이였습니다. 원래 필요한 용량의 2배였던 셈입니다.
이게 끝이 아닙니다. 위 프로그램에서 2개의 숫자가 한 줄에 나와 있었다는 것을 볼 수 있어요. 이것은 무엇을 의미할까요? 일단, a b가 나왔다는 것은, 이 시점에 배열의 capacity가 a에서 b로 늘어났다는 겁니다. 그런데, 이게 자기 마음대로 a에서 b로 늘어날 일은 없을 텐데. 어떻게 된 것일까요?
해답은 expand에 있습니다. 용량이 4였습니다. 4개가 다 찼습니다. 이 때, 또 push_back이 호출되었다고 해 봅시다. 그러면 공간이 부족해 질 거니까, 8개짜리 원소를 저장할 수 있는 배열이 생성이 될 겁니다.

이 과정을 그림으로 도식화 시키면 다음과 같습니다. 즉, 왼쪽에 출력된 수들의 합과 비례한 크기만큼 copy가 일어나고, delete가 일어납니다. 다음에, 오른쪽에 출력된 수의 합과 비례한 크기만큼 새로 할당이 됩니다. 그러면 최악의 경우에, 총 2^21 - 1개만큼의 원소를 저장할 수 있는 크기만큼 할당이 됩니다. 그리고 2^20 - 1번의 복사가 일어나고, 총 2^20 - 1개 만큼의 원소를 저장할 수 있는 크기만큼 delete가 됩니다.
단, 2^19 + 1번 push_back을 했을 뿐입니다. 1개의 원소의 크기만큼 공간을 삭제, 생성하는 데 cost가 1이 들고, 1개의 원소를 복사하는 데에도 1의 cost가 든다고 한다면, 대략 2^22의 cost가 듭니다. 대략 2^19 + 1회의 push_back이 호출되면. 2^22를 2^19로 나누면 8입니다. 최악의 경우, push_back을 호출할 때 평균적으로 8의 비용이 든다는 이야기입니다.

물론 최선에 가까운 경우, 2^19회 push_back을 호출했을 때 2^19 - 1개의 원소를 복사하고, 총 2^19 - 1개의 원소를 저장할 수 있는 배열의 크기만큼 삭제가 되고, 총 2^20 - 1개의 원소를 저장할 수 있는 배열의 크기만큼 생성이 됩니다. 1개의 원소 크기만큼 공간을 생성, 삭제하는 데 cost가 1이 들고, 1개의 원소를 복사하는 데에도 1이 든다고 해 봅시다. 이 때 총 cost는 대충 2^21이므로, 최선의 경우, 4 정도의 비용이 듭니다.
그런데, 대입을 하는 비용을 빼먹었습니다. 대입하는 데 드는 비용도 1이라고 가정하면, 최악의 경우 평균적으로 9, 최선의 경우 5의 cost만큼 듭니다. amortized O(1)일 뿐이지, 상수가 작다고 말할 수 없습니다.
그러면 어떻게 해야 할까요? 배열에 들어있는 원소의 최대 갯수를 미리 알 수 있다면, resize나 reserve를 호출하시면 됩니다. 아니면, 그냥 동적 할당으로 한번에 n개의 원소를 저장할 수 있는 배열을 만들면 됩니다. 이 둘은 어떻게 다를까요? 일단 기존의 capacity보다 더 크게 resize를 하거나, reserve를 해야 한다고 해 봅시다.

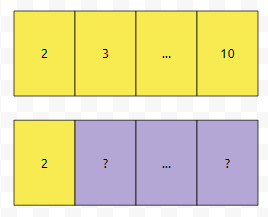
예를 들어, capacity가 4이고 size가 3인 경우를 생각해 봅시다. 그림으로 그리면 이런 상황입니다. ?라고 표시가 된 부분은 아직 값이 정해지지 않았다는 의미입니다. 여기서 reserve(6)을 호출하면 어떻게 될까요? 일단 4보다는 6이 크기 때문에, 새로운 공간이 할당이 될 겁니다.

그러면, 2, 3, 5는 새로운 배열에 copy가 될 겁니다. 그리고 기존에 있었던 작은 배열은 제거될 거에요. size는 변하지 않아요. 즉, [3]번째, [4]번째, [5]번째 원소는 아직 모릅니다. 즉, 새로운 배열의 [size]부터 [capacity-1]까지는 initialize가 되지 않습니다. 그러면, 아래 코드를 작성하고, wandbox에서 돌려보도록 하겠습니다.

i를 1부터 100까지가 아니라, 1부터 100만까지 돌리면 killed가 뜹니다. v.capacity()를 찍어보면 아래와 같이 출력이 됩니다.

1, 2, 3, 4, 5. 감이 오실 듯 싶어요. loop를 1번 돌 때 마다, 벡터의 용량이 증가하고 있습니다. 그런 걸로 봐서는, 루프가 한 번 돌 때 마다, 벡터의 size만큼의 복사가 일어나고, 새로운 배열도 할당이 되고, 기존의 배열도 삭제가 되는 연산이 일어나요. 아마, wandbox 내부의 구현체에서는 capacity보다 예약하는 공간이 크다면, capacity를 예약하는 공간의 크기에 딱 맞추는 모양입니다. 구현체에 따라 다를 수 있어요. 링크에 따르면, incrasing capacity n (or grater)라는 설명이 있어요. 이것은 딱 n을 맞추거나, 이보다 용량이 커질 수 있다는 것을 의미합니다. 저 같으면, n개의 공간을 예약하라고 하면, 딱 n개의 원소만 할당 가능하게끔 할 듯 싶어요.
resize를 호출한다면 이야기가 달라지는데요. size가 3이고 capacity가 4인 상황에서, resize(5,0)을 호출했다고 해 봅시다.

그러면 expand에 의해서, 새롭게 공간이 할당이 될 겁니다. 그리고 2, 3, 5. 그러니까 노란색 부분은 복사가 될 겁니다.
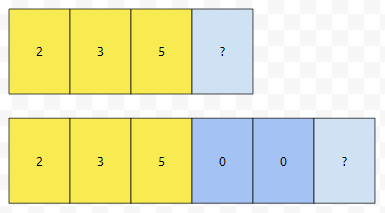
다음에 0은 [3]번째부터 [4]번째까지 들어갈 거에요. reserve와는 다르게 동작한다는 것을 알 수 있어요. 그러면 size보다 작게 resize를 한다면 어떻게 될까요? 역시 링크를 보시면, reduced n items, and removing beyonds. (and destroying them) 이라고 되어 있어요. 이 말을 잘 해석해 보면, 원래 벡터 안에 10개의 원소가 있었는데, resize(1)을 했다면, 1개는 남아 있습니다. 뒤에 있는 9개는 제거가 된다는 겁니다.
그럴려면 search를 해야 할 거에요.
위치 s에서부터 e까지 순회하는 데 시간 복잡도는 O(|e-s|)입니다. 물론, 제거가 되는 범위인 s에서부터 e까지 굳이 탐색도 하지 않고, 파괴도 하지 않을 수도 있습니다. 끝을 가리키는 포인터만 이동을 해도 문제가 없다는 것. 센스가 있으시다면 알아채실 수 있을 거에요. 그러면 이 둘은 언제 쓰면 좋을까요?
상수가 중요할 때, 그리고 시간 제한이 매우 빡빡할 때 고려해 볼 만 합니다. 그리고 크기를 아는 경우에. 크기를 모른다면, 어떻게 해야 할까요? 이 때에는 적당한 크기, 예를 들어 16, 32 등으로 초기 size를 잡아서 expand 연산이 덜 일어나게 하면 좋겠습니다.
'레퍼런스 > 분석' 카테고리의 다른 글
| c++ vector clear 함수 : size를 0으로 만들어 준다. (4) | 2020.03.21 |
|---|---|
| java deepequals 메서드 : 정말 깊게 비교한다. (4) | 2020.02.19 |
| java copyOf 메서드 : 배열을 복사한다. (5) | 2019.12.27 |
| java hashset은 key의 해쉬 코드가 모두 같을 때 최악 복잡도가 어떻게 될까요? (6) | 2019.12.18 |
| 왜 java에서는 equals 메서드를 오버라이드 하면 hashCode 도 같이 해야 할까요? (2) | 2019.12.15 |


최근댓글