저번에, 왜 equals를 구현하면 왜 hashCode를 같이 구현해야 하는지에 대해서 설명을 했습니다. hash 계열의 자료구조 때문에 그렇다고 했었습니다. 그렇지 않으면 어떻게 동작하는지는 여기를 참고하시면 좋겠습니다. 이 내용에 대해서 숙지하셨다고 가정하고 진행하도록 하겠습니다.
면접 질문에서 간혹 가다가 등장하는지는 잘 모르겠습니다만, 어떠한 객체의 hashCode 값이 같은 것들을 모두 hashSet에 넣을 때, 어떤 일이 벌어지는지는 꽤 중요한 문제 중 하나일 겁니다. 사실, 우리는 그렇게 바보같이 구현할 일이 없습니다. 그렇지만, 저는 이에 대해서 포스팅 하도록 하겠습니다. 먼저 Java 8에서부터, hashMap은 버킷에 8개 이상 달려있을 때, Balanced Tree로 변환이 된다는 것은 익히 들어서 알고 계실 겁니다. 그렇다면, 최악의 경우에 O(log(n))이 나올 거 같은데요. 정말 그럴까요?
아래 코드를 보겠습니다.
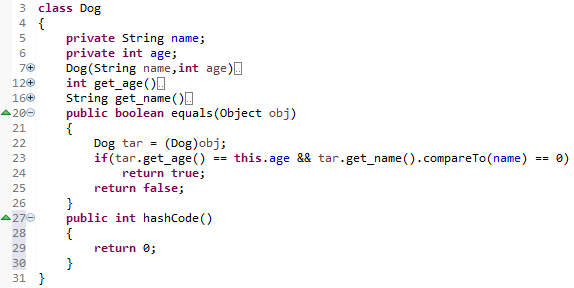
어제 했던 Dog 클래스를 그대로 가지고 왔습니다. 여기서 hashCode는 무조건 0을 리턴하게 되어 있습니다. 그러면, 0번 버킷에만 데이터가 skew가 될 겁니다. 너무 많이 충돌이 일어난다면, List 대신에 Tree로 변환을 할 거고요.

이제 10000개를 넣고, s.add(new Dog 객체)를 수행해 봅시다. 당연하게도, 내부적으로 putVal이 호출이 될 겁니다. 그리고, Tree이므로, 637번째 줄에 있는 else if문에 걸릴 겁니다.

그러면, 638번째 줄인, putTreeVal이 호출이 될 거에요. 여기서 잠깐 호출 스택만 짚고 넘어가 보겠습니다.

main, HashSet의 add, HashMap의 put, putVal, HashMap$TreeNode의 putTreeVal 이 순서대로 스택에 올라갔습니다. 이 함수에서, 중요한 코드들만 간단하게 보도록 하겠습니다.

먼저 putTreeVal이 호출이 되면, 길고 긴 if, else if, ... 문들이 보입니다. 여기서 p는 root의 hash값을, 매개변수로 넘어온 h는 내가 넣을 Dog 객체의 hash 값을 의미합니다. 당연하게도, 이 값은 오버라이딩이 된 hashCode의 리턴 값입니다. 그런데 이 값들이 모두 같다면, 1979번째 줄의 if와, 1981번째 줄의 else if문에도 걸리지 않을 겁니다.
여기서 잠깐. 1979번째 줄이나, 1981번째 줄의 조건을 만족하는 경우가 있을까요? hashCode 값이 어느 정도 적당히 있다고 했을 때. 이는 hashTable의 특성을 조금만 생각해 보면 어렵지 않게 답변할 수 있어요. hashMap의 Table size는 16, 32, 64, ... 이런 식으로 커진다고 해 봅시다.

만약에 bucket size가 32라고 해 봅시다. 그러면 hashCode 값이 32, 64인 것이 0번 버킷에 들어갈 겁니다. 이 상태에서, hashCode 값이 128인 친구가 들어갔다고 해 봅시다. 그러면 p.hash와 h가 다릅니다. 그러면 p.hash > h이거나, p.hash < h일 거에요. 그렇다면 1차 우선 순위는 HashCode의 값이다. 라는 것입니다.
객체의 해시값이 모두 0이라면, 당연하게도, 1979번째, 1981번째 if문이나, else if문에 걸리지 않을 거에요. 그러면서, equals가 다르다라는 결과를 리턴하면 어떻게 될까요?

그러면 1985번째 else if문에 있는 조건문들을 검사합니다. 여기서, kc가 null이면서, comparable하지 않다면, 1988번째 줄을 수행합니다. 그리고 tieBreakOrder 함수를 호출해서 dir 값을 갱신합니다. 그리고, searched 라는 것이 또 등장하는데요. 이것이 왜 등장했는지는 아래에서 설명해 드리도록 하겠습니다. 일단 여기까지 보도록 합시다.
조금 숨을 고르셨나요? 이제, find가 어떻게 동작하는지 보겠습니다.
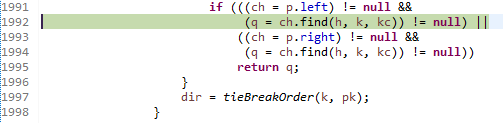
1992번째 줄에 있는 find를 호출해 봅시다. 이 때, 기준 위치는 root의 left입니다.

그러면 왠지 모르게, 되게 비슷비슷한 if, else if, ... 등으로 떡칠이 된 코드를 볼 수 있는데요. 사실 이들 중 대다수는 그렇게 중요하지 않습니다. 단지, 우리는 현재 기준 위치의 left와 right가 모두 있을 때에는 막바로 1874번째 줄로 간다는 것이 중요한 점입니다.

대충 이 지점입니다. 여기서 pr.find(~)를 호출하는데요. 이것의 의미를 되새겨 보도록 하겠습니다.

먼저 pr은, 현재 위치에서 오른쪽 자식을 의미합니다. 그러면 pr.find(~)는 무슨 의미일까요? pr을 루트로 하는 서브 트리에서 무엇인가를 찾겠다는 의미입니다.
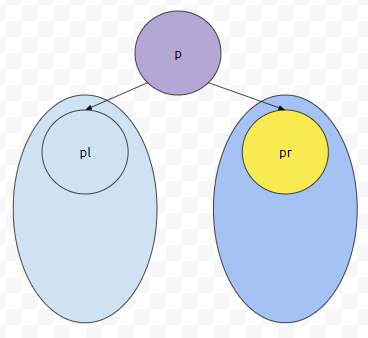
그러면 군청색으로 칠해진 노드들을 모두 탐색할 겁니다. 만약에 pr을 Subtree로 가지는 트리에서, 목표로 하는 무언가를 찾지 못했다면 어떻게 될까요? 이 때에는 pl의 값을 p에 넣습니다.
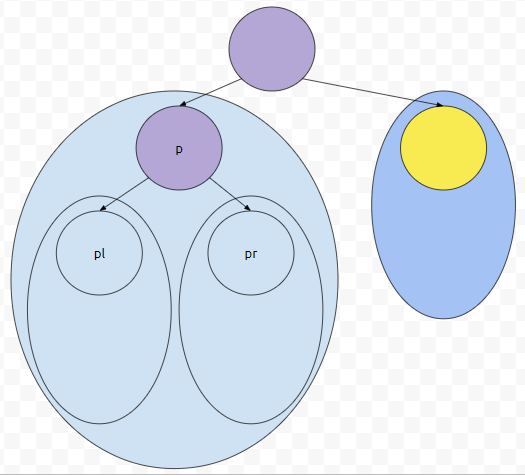
그러면 Left SubTree를 탐색할 겁니다. 어떻게 하면 되나요? 똑같이 우측부터 search 하면 됩니다.
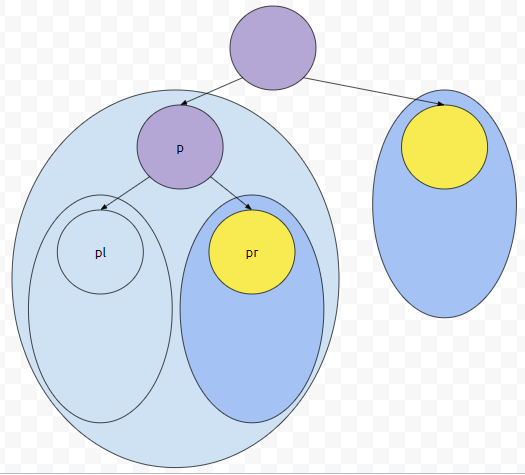
우측에서 찾아지지 않는다면 좌측에서 찾으면 됩니다. 뭔가 어떤 알고리즘을 본 거 같지 않으신가요? 전위 탐색, 중위 탐색, 후위 탐색. 이것과 매우 흡사하게 돌아갑니다. 이들은, 탐색을 시작한 점을 Root로 하는 서브 트리의 노드 수만큼 탐색합니다. 만약에 루트부터 탐색하고, 트리의 노드 수가 n이라면 복잡도가 O(n)인 셈입니다.

프로그램의 흐름도를 간단하게 표시하면 위와 같습니다.

그리고, binary Search Tree의 구조에 맞게 p를 재조정합니다. 이런 식으로, 추가될 위치가 나올 때 까지 for loop를 돕니다. 여기서 궁금한 점. 그러면 이 때, putTreeVal의 복잡도는 어떻게 될까요? 최악의 경우에 putTreeVal에서, find가 2*depth만큼 불릴 수 있지 않을까요? 사실 그렇지 않습니다. 1985번째 줄 주위를 다시 한 번 보겠습니다.
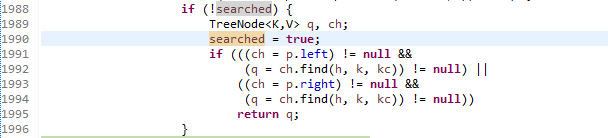
보시면 searched가 false일 때 1989번째 줄부터 수행이 됩니다. 그리고 1990번째 줄에 searched가 true가 됩니다. 이 시점에서, 다시 1988번째 if문을 수행하면 searched가 false가 아니므로, 바로 빠져나오게 됩니다. find가 2*depth만큼 호출되지 않습니다. 그렇기 때문에, Comparable을 implements를 하지 않고, compareTo를 오버라이드 하지 않은 경우에 hashCode 값까지도 모두 같다면 O(logn)이 아닌 O(n)의 복잡도를 가진다는 것을 알 수 있습니다.
그러면 비교 기준을 무엇으로 삼을까요? hashCode 값마저 같다면?
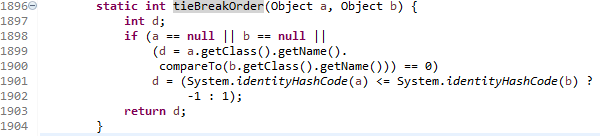
2개가 모두 Dog 객체였다면, identityHashCode 값으로 비교합니다. 이것을 가지고 균형 트리를 맞춥니다. 맞추는데, 이 두 값이 같은 경우도 있습니다. 이 때에는 -1을 리턴합니다.
만약에 Comparable<Dog>를 implements를 하고, compareTo를 오버라이딩 했다면 어떨까요?

당연하게도 compareTo는 둘이 equals 하다면 0을 리턴하게끔 작성했습니다. 이 때에는 다르게 동작합니다. 다시 putTreeVal을 보도록 하겠습니다. 1985 ~ 1987번째 줄의 else if문을 봅시다.

그러면, comparableClassFor이 null이거나, compareComparables, 그러니까 두 객체를 비교했을 때 compareTo의 값이 0이 아니라면, 바로 2000번째 줄로 건너뛸 거에요. 그런데 저는 <name, age>가 모두 같다면 equals가 true를 리턴하게 해 놓았습니다.

그렇기 때문에 1987번째 줄의 compareComparables 값이 true라면, 이미 1983번째 줄의 k.equals(pk) 조건에 걸렸을 거에요. 당연하게도 이 때에는 key 객체가 있다는 것이므로 hashMap이던 hashSet에 추가되지 않을 거에요. 이 작업을 depth만큼 반복하는데요. hashCode가 같은 Key 객체가 n개가 들어갔습니다. 이 때, 균형 트리의 depth는 O(log(n))에 비례하므로, 시간 복잡도는 기술 블로그 등에서 많이 언급되어서 익히 알려진 O(log(n))이 됩니다.
'레퍼런스 > 분석' 카테고리의 다른 글
| c++ vector reserve vs resize : 미리 공간을 만들어 놓고 쓰면 안 될까요? (12) | 2020.02.05 |
|---|---|
| java copyOf 메서드 : 배열을 복사한다. (5) | 2019.12.27 |
| 왜 java에서는 equals 메서드를 오버라이드 하면 hashCode 도 같이 해야 할까요? (2) | 2019.12.15 |
| 인트로 정렬 : c++의 sort는 왜 최악의 경우에도 빠르게 동작하는가? (4) | 2019.12.07 |
| c++ unique 함수 : 정렬을 먼저 해야 중복이 제거된다. (2) | 2019.11.28 |


최근댓글