크기가 5만 이하인 배열 array가 있습니다. 여기서, 연속적인 부분 배열들을 생각할 수 있습니다. 이 부분 배열에 속해있는 수들을 모두 bit or을 합니다. 그렇게 해서 나온 결과값들을 벡터 res에 담습니다. 벡터 res의 중복을 제거했을 때, res에는 몇 개의 수가 들어 있을까요? 즉, 연속적인 부분 배열들의 결과값이 될 수 있는 수의 갯수는 몇 개일까요? 단, 배열 안에 있는 수는 0이상, 10^9 이하의 정수 입니다. 예를 들어, [1, 3, 2]를 생각해 봅시다.

이 경우, 결과값이 될 수 있는 수는 1, 2, 3. 이렇게 3개입니다. 어떻게 풀면 좋을까요?
일단, 0이상, 10^9 이하의 정수라는 것은, 있을 수 있는 최대 상태 수가 30개라는 것입니다. 그러면, lo번째 위치에, 어떠한 수 x가 있다고 해 봅시다. 그러면 아래와 같은 Lemma가 성립합니다.

이것을 먼저 직관적으로 보여 봅시다. 어떤 수 A와 B를 bitwise or 했다고 생각해 봅시다. A의 t번째 위치에 있는 bit를 b1, B의 t번째 위치에 있는 bit를 b2라고 했을 때, b1과 b2의 값에 따라 b1 or b2의 값은 아래 표1과 같습니다.

여기서 주목해야 할 것은, b1의 상태가 0일 때, b1 or b2의 결과값은 0 또는 1이고, b1의 상태가 1일 때, b2의 값에 관계 없이 무조건 1이라는 것입니다. 즉, b1의 켜진 비트 위치를 집합 B1이라고 하고, b2의 켜진 비트 위치를 집합 B2라고 하고, b1 or b2의 켜진 비트 위치를 B3이라고 했을 때, B1은 B3에 포함되고, B2 또한 B3에 포함된다는 것입니다.
그러면 [lo, lo]를 모두 or한 결과값의 켜진 비트 집합은, [lo-1, lo]를 모두 or한 결과값의 켜진 비트 집합에 포함이 될 겁니다. 그리고 이것은, [lo-2, lo]를 모두 or한 결과값의 켜진 bit 집합에 포함될 겁니다. 우리는 이제 다음과 같은 상황으로 CONVERT를 할 수 있습니다.

카드가 4개 있습니다. 이 상태를 0000이라고 합시다. j>i라면, s(j)를 s(i)보다 먼저 선택하는 상황이 없다. 그러니까, 1개씩 뽑는다면 s1, s2, s3, s4 순서대로 뽑을 겁니다. 우리가 카드를 어떻게 잘 뽑았을 때, 상태가 많이 나오게 하려면 어떻게 하는 게 좋을까? 그리고 이 때에는 몇 가지의 state가 나올까?
일단, 카드를 안 뽑는다면, 상태가 변하지 않아요. 그렇기 때문에, 뽑는 것이 이득일 겁니다.

s1만 뽑았습니다. 1이 뽑혔기 때문에, state는 0000에서 1000이 됩니다. 다음에는 어떻게 뽑을까요?

2와 3을 뽑아봅시다. 그러면 1000에서 1110이 될 겁니다. 그런데, 사실 이 때에는 s2, s3 둘 다 뽑는 게 아니라, s2만 뽑았다면, state 수를 조금 더 많이 만들었을 수도 있었을 겁니다.

즉, s2만 뽑으면, 이 때 상태는 1100인데요. 그 다음에 s3을 뽑는다면 1100에서 1110으로 만들 수 있기 때문입니다.

이 상태에서, s4를 뽑으면 1111이 됩니다.

즉, 나올 수 있는 상태는 최대, 4+1개가 됩니다. 0000, 1000, 1100, 1110, 1111. 이것은 상태 bit를 4개만 쓸 때의 이야기입니다. 배열에 들어 있는 수의 범위를 보았을 때, 필요한 비트의 수는 30개임을 알 수 있어요. 써야 하는 bit의 수가 30개이므로, 어떠한 끝점 e를 기준으로 보았을 때, 나올 수 있는, [i, e]의 구간 or 정수 값은 많아봐야 31개임을 알 수 있습니다.
그러면 많아봤자 31개를 어떻게 빠르게 구할까요? 우리는 가능한 [i,lo]의 구간 or 답의 집합을 알기 위해서, [i,lo-1]의 구간 or 집합을 끌어올 필요가 있음을 직관적으로 알 수 있습니다.

노란색 부분을 구간 or한 것이 집합 P에 포함되어 있습니다. 그러면 여기에 보라색 구간인 arr[lo]를 or 하면 됩니다.

이것도 마찬가지인가요? 노란색 부분을 구간 or 한 것이 집합 P에 포함되어 있을 때, 이것과 arr[lo]를 or하면 된다는 것을 알 수 있어요. 우리는 [i,lo-1]의 bit or 결과값 가능 집합 P를 알고 있을 때, [i,lo]의 bit or 결과값 가능 집합을 구할 수 있습니다. 단지, P를 순회함으로서, C를 구할 수 있습니다. 그리고 C에는 arr[lo]도 들어가야 된다는 것을 잊어버리면 안 됩니다. 이것을 그대로 코드로 구현하면 아래와 같습니다.

먼저 P를 토대로, C를 구축하고 있습니다. 그리고 C에 A[i]도 넣고 있어요. 다음에, C를 정렬한 다음에, 중복된 원소를 제거하고 있습니다. 그러면, C의 size는 많아봤자 31개일 겁니다.

P를 clear하고, 구축되어진 C를 돌면서 R에 넣습니다. 그리고 P에도 넣습니다. 이는 결과를 의미합니다. 결과값에 다 반영한 후에는 C가 필요 없으므로, C를 clear 시킵니다. 그리고 for loop를 모두 돈 다음에 R을 sort 한 다음에, 중복을 제거합니다. 중복을 제거한 R의 size가 답이 되므로, R.size()를 return 합니다.
n번 loop를 돌 때 마다 최대 31log31, 그리고 대략 31n개의 원소를 정렬하기 때문에, 이 코드는, O(31nlog(31n))이 됩니다. 31n은 155만보다는 작으므로, 실행 시간은 대략적으로 유추만 해 보시면 됩니다. 650ms 정도 나왔습니다.
이것을 빠르게 하는 방법은, R을 sort로 정렬하는 것이 아니라, radix sort로 정렬하면 됩니다. 65536 진법으로 정렬한다면, O(n)에 sort가 되므로, O(31nlog(31n))을 O(31nlog31)으로 줄일 수 있습니다. 그런데, 이것 말고 더 줄일 수 있는 방법이 없을까요?

for loop 안의 코드를 보면, C를 정렬하는 코드가 사라져 있음을 알 수 있어요. 정말 그렇게 해도 될까요? 정답은 그렇게 해도 된다. 입니다. 왜 그럴까요? P에 어떻게 데이터가 들어갔을 지를 생각해 봅시다.

일단 arr[lo-1]의 값을 r1이라 합시다.
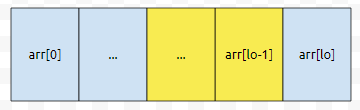
그리고 노란색으로 칠한 부분을 모두 bit or한 값을 r2라 합시다. r1 <= r2일 겁니다. 왜냐하면, arr[lo-1]의 켜진 비트들은, 노란 구간 내에서 최소한 1번 이상 켜져있음이 자명하기 때문입니다. 그리고 ...과 arr[lo-1]을 묶어서 하나의 수 r2로 생각할 수 있어요.

그러면 앞에 ... 구간과 r2를 bit or 하면 어떻게 될까요? r2의 켜진 비트들은, r2에서 켜졌거나, ...에서 켜졌을 겁니다. 최소 1번은 켜졌기 때문에, 노란 부분을 모두 bit or한 값을 r3이라 한다면 r2 <= r3일 겁니다.

그러면, P에 저장된 값들을 봅시다. 제가 [a(1), lo-1] 이런 식으로 표시해 놓았는데요. 이것은 구간 [a(1), lo-1]을 모두 bit or한 값을 의미합니다. 물론 중복 제거하면서 sort한 결과이고요. 그러면, a(1) > a(2) > ... > a(s)일 거고, a(1) <= lo-1일 겁니다. 이것은 당연한 이야기입니다.
그러면, 이것을 토대로, 구간 [i, lo]의 bit or한 정보들을 모두 채워서 sorting을 한다고 가정해 봅시다. 그러면

[a(1), lo]는 [a(1), lo-1]의 값에, arr[lo]를 or한 값일 겁니다. 이것은 구간 [a(1), lo]에 있는 수들을 bit or한 값입니다. 그러면 구간 [lo, lo]는 구간 [a(1), lo]에 포함이 됩니다. 왜냐하면 a(1) <= lo-1이기 때문입니다. 그렇다면, cleared된 C에 먼저 A[i]를 넣고, 다음에, A[i]와 P[j]를 or한 값을 넣으면 sort할 필요 없이 크기 순으로 정렬이 됩니다.
그러면, loop마다 O(31log31) 정렬을 수행할 필요 없이 선형 탐색 몇 번 하면 됩니다. 그리고 이것을 토대로 radix_sort를 하면, 특정 데이터에 관계 없이 O(31n)만에 수행할 수 있습니다. 전체 코드는 제 github에 올려져 있습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 등차수열에서 중간에 빠진 수 구하기 : binary search 기법으로 풀면 된다. (4) | 2019.12.10 |
|---|---|
| 백준 회의실 배정 : 가능한 space를 최대한 크게 만들자. (6) | 2019.11.27 |
| leetcode 338 counting bits : 마지막 켜진 비트만 알면 된다. (6) | 2019.11.22 |
| 바빌로니아 법 알고리즘 : 어떻게 sqrt 함수를 구현할까요? (11) | 2019.11.20 |
| 바이토닉 정렬 : 엇갈려 가면서 sorting 한다. (8) | 2019.11.02 |


최근댓글