제가 제대로 된 코딩을 한 지 별로 안 되서 그런지, 백준 1442번 같은 문제를 만나면 당황스럽더라고요. 문제는 다음과 같습니다.

부끄럽게도, 어떻게 Dynamic programing을 해서 트래킹을 해야 할 지 감이 오지 않았습니다. 그러면 어떻게 해야 할까요? 손을 놓고 가만히 있어야 할까요? 아닙니다. 정확하게 문제를 앞쪽, 뒤쪽으로 나누었을 때, 적절한 전처리를 해서, 앞쪽만 보고 접근할 수 있다면, 양방향 탐색과 유사한, 중간에서 만나는 meet in the middle 이라는 기법을 고려해 볼 만 합니다.
코딩 테스트에서 제일 중요한 것은 문제를 어떻게 읽느냐였다고 했습니다.

앞에 15개, 뒤에 16개로 왜 나눌까요? 일단, 그 전에 R - L이 20만 이하인 경우부터 해결해 봅시다.

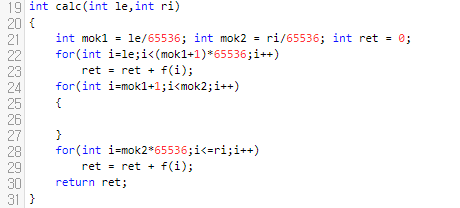
먼저, 해당 수가 이진수로 나타냈을 때, 멋진 수이면 1을, 아니라면 0을 리턴하는 함수를 f라고 합시다. work 함수는 le에서 ri까지 멋진 수의 갯수가 몇 개나 있는지를 돌려준다고 하고요. 그러면, work 함수는, le부터 ri까지 돌면서 f 메서드를 계속 호출하면서 ret에다가 f의 리턴값을 더해주면 될 겁니다.
f 함수를 보겠습니다.

먼저, x를 2진수로 변환해서 vector에 저장합니다. 다음에, dp[x]를 x번째 위치가 수가 몇 번 연속되어 있는지로 정의합니다. dp[0]은 당연하게도 1입니다.

그러면 dp[i]를 어떻게 채우면 되나요? 이전 것과 현재 것이 같으면, dp[i-1] + 1을, 그렇지 않으면 dp[i] = 1로 갱신해 주면 됩니다. 그리고, mmx는 연속된 연쇄의 최댓값을 저장하고 있기 때문에, mmx가 3보다 크거나 같다면 1을 리턴해 주면 됩니다. 이 부분은 그렇게 어렵지 않습니다.
문제는 R - L이 1억, 2억 이렇게 클 때인데요. 이 때, meet in the middle 알고리즘을 적용합니다. 먼저, R - L이 20만보다 크다면, 최소한 3구간 이상은 계산을 해야 한다는 것을 알 수 있어요. 그러면 큰 설계는 다음과 같이 할 수 있습니다.
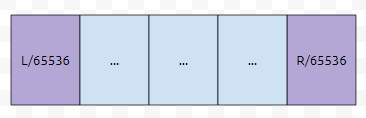
먼저 L이 속해 있는 [L/65536]번 구간과 R이 속해있는 [R/65536]번 구간은 그냥 브루트 포스를 돌려도 될 듯 싶습니다.
문제는 중간에 껴 있는 구간들입니다. 이 부분은 어떻게 처리해야 할까요?

먼저 앞 부분이 멋진 수라면, 이것은 볼 필요도 없습니다. 뒷 부분이 0..0이던 1..1이던 멋진 수인 것은 자명합니다. 따라서 이 때는 그냥 65536을 더하면 됩니다. 그렇지 않다면 어떻게 해야 할까요? 일일히 다 해 봐야 할까요? 네. 그런데 정말 일일히 다 하면 시간 초과 나기 딱 좋습니다. L이 1이고, R이 2147483647일 때, 2582개의 구간에 대해서 일일히 다 봐야 하는데, 2582에 65536을 곱하면 약 1.69억입니다. 이 후보해들에 대해서 일일히 다 보면 당연하게도 시간 초과입니다.
실제로 이 때 답은 2.1억보다는 큽니다. 각 후보해에 대해서 O(1)의 복잡도로 본다고 해도 아슬 아슬하거나 시간 초과가 날 수 밖에 없어요. 어떻게 개선해야 할까요? 아이디어는 간단합니다.

앞에 부분이 10으로 끝나면서 ?10이 멋진 수가 아닐 때. 즉, 끝 부분만 보았을 때, 0이 1번 연속하는 경우가 있습니다. 이 때, 뒤에 부분을 적절히 잘 채웠을 때 멋진 수가 되는 가짓수는 2^16번 check를 하면 구할 수 있습니다.
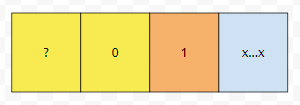
그 다음에, 앞에 부분이 01로 끝나면서 ?01이 멋진 수가 아닐 때. 즉 끝 부분만 보았을 때, 1이 1번 연속하는 경우가 있습니다. 이 때 뒤에 부분을 적절하게 잘 채웠을 때 멋진 수가 되는 가짓수 역시 2^16번 check를 하면 구할 수 있어요. 이 두 상태는 위상으로 보았을 때, 사실상 동일하다는 것을 알 수 있습니다. 왜 그런지 곰곰히 생각해 보셔도 도움이 되실 듯 싶습니다.
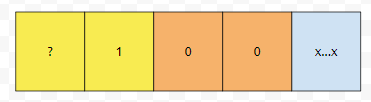
3번째 경우는 ?100으로 끝나면서 ?100이 멋진 수가 아닌 경우가 있습니다. 이 때, 뒤에 부분을 잘 채워서 멋진 수가 되는 가짓수도 2^16개의 수만 잘 체크하면 구할 수 있어요.

4번째 경우는 ?011로 끝나면서, ?011이 멋진 수가 아닌 경우가 있습니다. 이 때, 뒤에를 잘 채워서 문제의 조건에 맞는 수가 되는 가짓수 또한 2^16개의 수만 체크하면 구할 수 있어요. 여기서 ? 부분은 고려를 안 해도 됩니다. 4가지 경우 모두 ? 부분은 고려를 하지 않아도 됩니다. ?가 있던 없던 뒤에 부분이 어떻게 채워지느냐에 따라서, 멋진 수인지 아닌지가 결정이 되기 때문입니다.
3번째와 4번째 역시 위상이 동일하다는 것을 알 수 있는데요. 왜 그런지는 제가 따로 설명을 하지는 않겠습니다. 1, 2의 위상이 같고, 3, 4의 위상이 같다는 점을 이용해서, 저는 g를 정의하겠습니다.

이것까지 정의하고 나면, 보라색 구간 외에 나머지 구간을 효율적으로 처리할 수 있습니다.
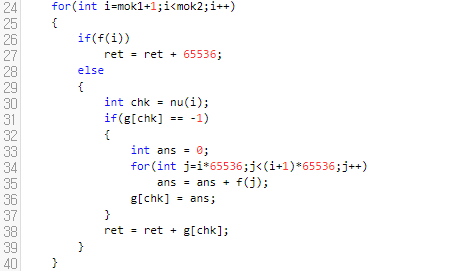
즉, 2개의 부분으로 나누었을 때, 시간 내에 돌 거 같다. 그러면 Meet in the middle 알고리즘을 고려해 볼 만 합니다. 약간 양방향 탐색하고도 유사한 부분인데요. 어떻게 다른지는 다소 어려운 이것과, 이 문제와, 이 문제를 풀어보시면 감이 오실 듯 싶습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 코테에서 답을 미리 저장하는 방법도 쓸만한가요? 네 (4) | 2020.01.29 |
|---|---|
| 프로그래머스 가장 큰 수 : 수 2개만 고려해 봅시다. (7) | 2020.01.24 |
| 백준 11691 lcm(i,j) : lcm과 gcd의 관계를 이용한 역발상이 필요하다. (8) | 2019.12.31 |
| 백준 팰린드롬 진법 : 후보해는 생각보다 많이 적다. (10) | 2019.12.21 |
| 힙 정렬 (heap sort) : 최악의 경우에도 O(nlogn)이다. (2) | 2019.12.19 |


최근댓글