수학적으로 잘 설명된 포스팅은 많으니, 저는 ps 문제를 풀도록 하겠습니다. 백준 1649번 문제를 보겠습니다. 문제를 간단하게 요약하면 다음과 같습니다. 도시가 1000개 있습니다. 일방통행이 되는 도로 M개가 주어집니다. 중간 지점은 k개, C(1), ... , C(k)가 있다고 하겠습니다. A에서 출발해서 중간 지점들을 모두 거쳐서 B로 가고자 할 때, 가능한 경로의 가짓수를 구하는 것이 문제입니다.
a에서 b까지 가는 도로는 최대 1개만 존재하고, 어떠한 교차로에서 출발해서, 다시 그 교차로로 돌아올 수 없다는 조건이 주어졌는데, 왜 이런 조건이 주어졌는지는 잘 모르겠습니다.
중간 지점들을 방문하는 순서는 정해진다는 관찰을 하면, 이 문제는 난이도가 상당히 쉬워 집니다. 이 관찰이 유효한 것인지 보도록 하겠습니다. 그 전에, 서로 다른 두 순열 (permutation)을 생각해 보도록 하겠습니다.
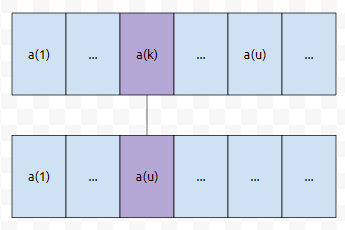
보라색으로 칠한 부분에서 최초로 달라진다고 해 보겠습니다.

이전의 permutation에서는 a(k)가 a(u)보다 앞에 나왔을 겁니다. 그런데, 바뀐 permutation에서는 a(u)가 앞에 나왔습니다. 어랏? 즉, a(u)가 노란색 부분들보다는 앞으로 간 것이 자명합니다. 순서가 역전되었다고(reversed) 이야기 하겠습니다. 같은 순열이 아닌데, 순서가 모두 바뀌지 않을 수는 없습니다.

만약에 그렇게 된다면, 두 perm은 같은 순열일 겁니다.
그러면, 중간 교차로를 방문하는 순서가 반드시 정해진다는 말은 무슨 말일까요? 명제 p를 부정한 것이 참인지 보겠습니다. 중간 교차로를 방문하는 순서가 둘 이상 발생한다고 해 보겠습니다. 이는 p를 부정한 것입니다.
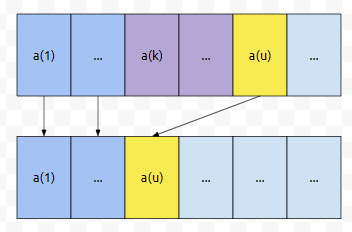
이 말인 즉슨, 순서가 뒤바뀌는 경우가 생긴다는 것입니다. 두 순열을 보았을 때, 군청색 부분은 모두 같았다고 해 보겠습니다. 위에서 부터 봅시다. 위 perm은 a(1)에서 a(k)로, 그리고 a(k)에서 a(u)로 방문하는 경로가 있었습니다. 이것을 그래프로 그려보면 아래와 같습니다.

2번째 perm을 보면, a(u)에서 a(k)로 가는 경로가 있다는 것을 추론할 수 있습니다. 왜냐하면, 군청색으로 칠한 부분은 순서가 바뀌지 않았고, 그 다음에 바로 a(u)가 온 상황입니다.

만약에, a(u)와 a(k)의 순서가 바뀌지 않았다면, a(k)는 군청색 부분에 등장했어야 했습니다. 그런데, 위에 있는 순열에 따르면, 군청색 부분에 a(k)가 있었다면, a(k)가 2번 이상 나타났을 겁니다. 모순이 생겨버립니다. 따라서, a(u) 다음에 a(k)가 나올 수 밖에 없어요. 이 관계까지 그래프에 반영해 보면 아래와 같습니다.
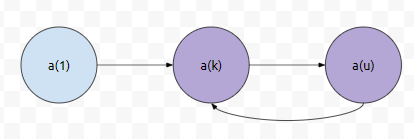
그랬더니 어떤가요? 사이클이 생겨버렸습니다. not p가 참임을 가정했을 때, 모순이 생겨버렸습니다. 따라서, 중간 교차로를 방문하는 순서는 반드시 하나로 강제된다는 명제 p는 참입니다.

저는 귀류법의 원칙을 그대로 따랐을 뿐입니다.
문제 난이도가 꽤 낮아졌지만, 그렇다고 해서 쉽다는 것은 아닙니다. 아직 처리해야 할 것들이 남아 있습니다.

(1) 먼저 해결해 보겠습니다. A에서 출발했을 때, 도달할 수 없는 것들은 모두 0 처리 합니다. 이것은, A에서부터 bfs를 돌려서, visit 되지 않은 정점만 따로 체크하면 될 거에요.

다음에, a(1), ... , a(k)에서 u(1)로 가는 경로가 있다고 합시다. 그러면, u(1)까지 가기 위해서 경유지를 몇 개 거쳐야 하는지 어떻게 계산하면 될까요? a(1)까지 도달하는 데 b(1)개의 경유지를 거쳐야 한다고 해 봅시다. 그리고 a(2)까지 가려면 b(2)개, ... , a(k)까지 도달하려면 b(k)개를 거쳐야 한다고 했을 때, u(1)까지 도달하기 위해서는 max(b(1), ... , b(k))에다가, u(1)이 중간 경유지라면 1을 더하고, 그렇지 않으면 0을 더하면 될 겁니다.

이를 수행하는 코드는 calc 함수입니다. 몇 개의 경유지를 도달해야 하는지에 대한 정보를 구했다면, 실제 가짓수를 구하는 것은 크게 어렵지 않습니다.

먼저 u(1)이 경유지라면, u(1)과 역간선으로 연결된 도시들에 대해서, 거쳐가야 하는 경유지 수가 d-1인 것들만 고르면 됩니다. 만약에 경유지가 아니라면 어떻게 하면 될까요?

u(1)과 역간선으로 연결된 도시들 중에서, 거쳐가야 하는 경유지 수가 d인 것들만 고르면 됩니다.

calc2 함수를 간단하게 보겠습니다. 크게 어려운 것은 없습니다. visit[x]값이 0이면 0을 바로 리턴해 버립니다. 그리고 x가 시작점이면, 1을 리턴합니다. dp2[x]가 -1이 아니면 그냥 dp2[x]를 리턴합니다.

86번째 줄에 있는 for문은 헷갈리기 쉬운데요. 사실 별 거 없습니다. 조건에 맞는 valid한 경로만 판단해서 가짓수에 더합니다. 이 정도만 판단하시면 크게 어려운 것은 없습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 카카오 호텔 방 배정 : map 을 이용해서 깔끔하게 처리합시다. (0) | 2020.05.09 |
|---|---|
| event driven : ps 문제에서 간단하게 활용해 봅시다. (0) | 2020.05.01 |
| 항등식으로 구현체를 외울 수 있는 확장 유클리드 알고리즘 (2) | 2020.04.09 |
| 백준 공유기 설치 : 왜 이분탐색이 가능한가? (0) | 2020.03.27 |
| 플로이드 알고리즘 : 어떻게 최단거리가 갱신되는가? (9) | 2020.03.03 |


최근댓글